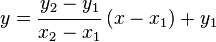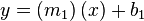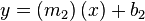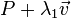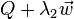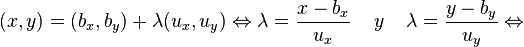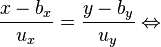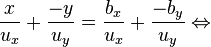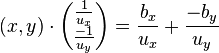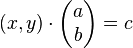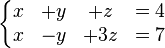2. FORMAS DE LA ECUACIÓN DE LA RECTA
Definición de linea recta
La línea recta es uno de los conceptos fundamentales en la comprensión de la asignatura de la Geometría Analítica, algunos de los más utilizados son:
1. Una línea recta es el lugar geométrico en un plano formado por una sucesión de puntos que tienen la misma dirección. Dados dos puntos diferentes, sólo una recta pasa por esos dos puntos.
2. Es el lugar geométrico de los puntos de un plano, de los cuales al tomar dos cuales quiera, el valor de la pendiente m, es siempre constante.
3. Es el lugar geométrico formado por un polinomio de primer grado de la forma y= a0 + a1x.
4. Es el lugar geométrico obtenido al unir dos puntos, tal que la distancia recorrida, es la más corta posible.
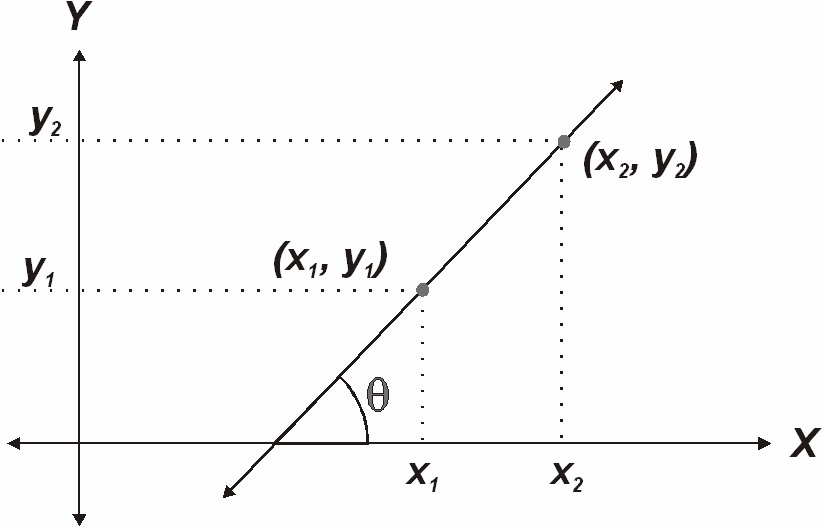
Como veremos la ecuación de una linea recta se puede presentar de varias formas, las cuales estudiaremos en este bloque.
Pregunta de Elección Múltiple
Recta
En geometría euclidiana, la recta o la línea recta se extiende en una misma dirección por tanto tiene una sola dimensión y contiene infinitos puntos; se puede considerar que está compuesta de infinitos segmentos. Dicha recta también se puede describir como un sucesión continua e indefinida de puntos extendidos en una sola dimensión, es decir, no posee principio ni fin.
Es uno de los entes geométricos fundamentales, junto al punto y el plano. Son considerados conceptos apriorísticos ya que su definición solo es posible a partir de la descripción de las características de otros elementos similares. Un ejemplo de las dificultades de la definición de la recta a partir de puntos es la llamada paradoja de Zenón de la dicotomía que ilustraba la desaparición de la recta al dividirla en puntos. Así, es posible elaborar definiciones basándose en los postulados característicos que determinan relaciones entre los entes fundamentales. Las rectas se suelen denominar con una letra minúscula.
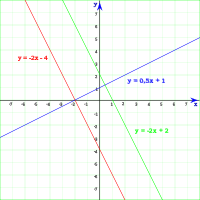
En geometría analítica las líneas rectas pueden ser expresadas mediante una ecuación del tipo y = m x + b, donde x, y son variables en un plano cartesiano. En dicha expresión m es denominada la "pendiente de la recta" y está relacionada con la inclinación que toma la recta respecto a un par de ejes que definen el plano. Mientras que b es el denominado "término independiente" u "ordenada al origen" y es el valor del punto en el cual la recta corta al eje vertical en el plano.
Índice
- 1 Definiciones y postulados de Euclides relacionados con la recta
- 2 Características de la recta
- 3 Ecuación de la recta en el plano
- 3.1 Pendiente y ordenada al origen
- 3.2 Forma simplificada de la ecuación de la recta
- 3.3 Forma segmentaria de la ecuación de la recta (ecuación simétrica)
- 3.4 Ecuación general de la recta
- 3.5 Ecuación normal de la recta (primera forma)
- 3.6 Ecuación normal de la recta (segunda forma)
- 3.7 Rectas que pasan por un punto
- 3.8 Recta que pasa por dos puntos
- 3.9 Rectas notables
- 3.10 Rectas en el plano como espacio vectorial y afín
- 4 Ecuación de la recta en el espacio
- 5 Véase también
- 6 Notas
- 7 Referencias
- 8 Enlaces externos
Definiciones y postulados de Euclides relacionados con la recta[editar]
Euclides, en su tratado denominado Los Elementos,[1] establece varias definiciones relacionadas con la línea y la línea recta:
- Una línea es una longitud sin anchura (Libro I, definición 2).
- Los extremos de una línea son puntos (Libro I, definición 3).
- Una línea recta es aquella que yace por igual respecto de los puntos que están en ella (Libro I, definición 4).
Características de la recta[editar]
- La recta se prolonga indefinidamente en ambos sentidos.
- En geometría euclidiana, la distancia más corta entre dos puntos es la línea recta.
- La recta puede definirse como el conjunto de puntos situados a lo largo de la intersección de dos planos.
Semirrecta[editar]
Se le llama semirrecta[nota 1] a cada una de las dos partes en que queda dividida una recta al ser cortada en cualquiera de sus puntos. Es la parte de una recta conformada por todos los puntos que se ubican hacia un lado de un punto fijo de la recta, denominado origen, a partir del cual se extiende indefinidamente en una sola dirección.
Semirrecta opuesta[editar]
La semirrecta opuesta de una semirrecta es la otra semirrecta salida de la recta que define la primera.[5] [6]
- Cada semirrecta solo tiene una semirrecta opuesta.
- Una semirrecta y su semirrecta opuesta tienen el mismo origen.
Ecuación de la recta en el plano[editar]
En un plano cartesiano, podemos representar una recta mediante una ecuación general definida en dicho plano ya sea mediante coordenadas usando puntos y vectores, o bien funciones que especifican dichas coordenadas.
Pendiente y ordenada al origen[editar]
Dada una recta mediante un punto, , y una pendiente
, y una pendiente 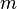 :
:
Se puede obtener la ecuación de la recta a partir de la fórmula de la pendiente (ecuación punto-pendiente):
donde 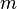 es la tangente del ángulo que forma la recta con el eje de abscisas X.
es la tangente del ángulo que forma la recta con el eje de abscisas X.
Ejemplo[editar]
La ecuación de la recta que pasa por el punto 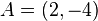 y que tiene una pendiente de
y que tiene una pendiente de 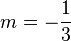 :
:
| Demostración |
|
Al sustituir los datos en la ecuación, resulta lo siguiente:
|
Forma simplificada de la ecuación de la recta[editar]
Si se conoce la pendiente m, y el punto donde la recta corta al eje de ordenadas es (0, b), podemos deducir, partiendo de la ecuación general de la recta,  :
:

|
Esta es la segunda forma de la ecuación de la recta y se utiliza cuando se conoce la pendiente y la ordenada al origen, que llamaremos  .
.
Forma segmentaria de la ecuación de la recta (ecuación simétrica)[editar]
Recta que corta el eje ordenado en  y la abscisa en
y la abscisa en  .
.
 .
.
| Demostración |
|
Si se plantea como problema encontrar la ecuación de una recta, conocidos
Con estos puntos se puede encontrar dicha ecuación, pero primero se debe calcular la pendiente:
Después se sustituye en la ecuación
y dividinedo toda la ecuación entre el término independiente
Se obtiene la ecuación de la recta en su forma simétrica. Esta ecuación se suele utilizar para obtener la ecuación de una recta de la que se conocen sus intersecciones con los ejes y cuando, a partir de la ecuación de una recta, se desean conocer los puntos donde dicha recta interseca a los ejes. |
Ecuación general de la recta[editar]
Es la expresión Ax + By + C = 0,[10] -A/B representa la pendiente y -C/B señala la ordenada en el origen cuando B sea diferente a cero. Datos suficientes para representar cualquier recta en el plano cartesiano XOY.
Ecuación normal de la recta (primera forma)[editar]
La forma normal de la recta (Ecuación de Hesse):
Siendo d el valor de la distancia entre la recta y el origen de coordenadas. El ángulo omega ω es el ángulo entre la perpendicular a la recta y la parte positiva del eje de ordenadas.[11]
Si en lugar del ángulo de la normal ω se emplea el ángulo de la recta α, entre la recta y el eje de las ordenadas:
Siendo d el valor de la distancia entre la recta y el origen de coordenadas. El ángulo alfa α es el ángulo entre la recta y la parte positiva del eje de ordenadas, cuya tangente expresa el valor de la pendiente de la recta.
| Demostración |
|
Para obtener dicha ecuación a partir de una ecuación de la forma al dividir los parámetros de la ecuación por |
Ecuación normal de la recta (segunda forma)[editar]
 |
Tomando el valor positivo o negativo de la raíz según corresponda.
Rectas que pasan por un punto[editar]
Para determinar las rectas del plano que pasan por el punto  se usa la ecuación
se usa la ecuación
 donde m toma cualquier valor real.
donde m toma cualquier valor real.
| Demostración |
|
La ecuación de la recta ha de ser: Y ha de pasar por el punto Despejando b, tenemos esta ecuación: Sustituyendo b en la ecuación general de la recta: Ordenando términos: Esta ecuación define un haz de rectas en el plano que pasa por el punto |
Recta que pasa por dos puntos[editar]
Si pasa por dos puntos  y
y  , la ecuación de la recta puede expresarse como:
, la ecuación de la recta puede expresarse como:
| Demostración |
|
Han de cumplir la fórmula general eliminamos la incógnita b, despejando en la primera ecuación y sustituyendo en la segunda: agrupando términos: despejando m: este valor, m, es el de la pendiente de la recta que pasa por los dos puntos: y sustituyendo m, por su valor ya calculado; Tenemos las dos incógnitas m y b despejadas, en función de las coordenadas de los dos puntos por los que tienen que pasar, entonces la ecuación general de la recta, con los parámetros ya calculados es: |
Rectas notables[editar]
- La ecuación de una recta vertical responde a la ecuación general
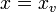 (constante).
(constante).
- La ecuación de una recta horizontal responde a la ecuación general
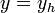 (constante).
(constante).
- Una recta trigonoidal que pase por el origen O (0, 0), cumplirá la condición b = 0, siendo su ecuación:
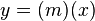 .
.
- Dos rectas cualesquiera:
- serán paralelas si y solo si
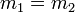 . Además, serán coincidentes cuando:
. Además, serán coincidentes cuando: 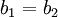
- serán perpendiculares si y solo si
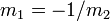 , es decir:
, es decir: 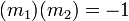
Rectas en el plano como espacio vectorial y afín[editar]
Mediante dos puntos del plano afín[editar]
Dado dos puntos en el plano, P y Q, sobre una recta, se puede describir cada punto de ésta es decir toda la recta mediante la ecuación:
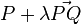 donde
donde 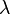 puede tomar cualquier valor.
puede tomar cualquier valor.
Ejemplo[editar]
Dados 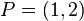 y
y 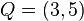 , entonces la recta son los puntos
, entonces la recta son los puntos 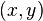 tales que
tales que 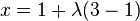 y
y 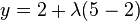 .
.
Mediante un punto y un vector[editar]
Dado un punto y un vector en el plano, P y 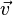 , queda totalmente definida una recta mediante la ecuación:
, queda totalmente definida una recta mediante la ecuación:
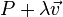 donde
donde 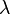 puede tomar cualquier valor.
puede tomar cualquier valor.
Ejemplo[editar]
Dados 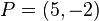 y
y 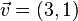 (llamado vector director), entonces la recta son los puntos
(llamado vector director), entonces la recta son los puntos 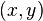 tales que
tales que 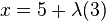 y
y 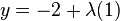 .
.
Rectas notables[editar]
- La ecuación de una recta vertical poseería un vector director del tipo
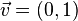 .
.
- La ecuación de una recta horizontal poseería un vector director del tipo
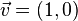 .
.
- Una recta por el origen, es una recta que pasa por el origen de coordenadas con
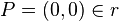 .
.
- Dadas dos rectas cualesquiera
- serán paralelas si y solo si
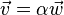 .
.
- serán perpendiculares si y solo si
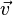 y
y 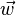 son perpendiculares, es decir su producto escalar es cero.
son perpendiculares, es decir su producto escalar es cero.
Rectas como producto escalar[editar]
Toda recta ya sea de forma implícita, explicita o vectorial se puede expresar como producto escalar de vectores:
es decir, renombrando las constantes:
- Si
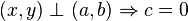 por tanto el vector
por tanto el vector 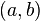 es perpendicular a la recta
es perpendicular a la recta 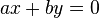 y a sus vectores directores, y por tanto a todas sus paralelas.
y a sus vectores directores, y por tanto a todas sus paralelas.
Ecuación de la recta en el espacio[editar]
Recta determinada mediante un sistema de ecuaciones[editar]
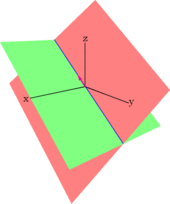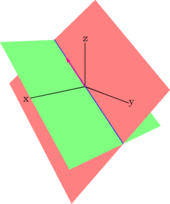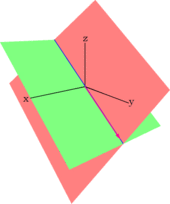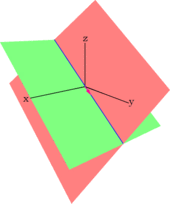
Recta en el espacio usando un sistema de 2 ecuaciones y 3 incógnitas:
- Esta ecuación equivale a la intersección de dos planos en el espacio.
Recta determinada mediante vectores[editar]
Recta en el espacio usando un punto, 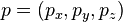 , y un vector,
, y un vector, 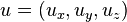 :
:
- Al vector
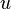 se le llama vector director.
se le llama vector director.
Posiciones relativas entre rectas[editar]
- Dos rectas serán paralelas si tiene vectores directores paralelos.
- Dos rectas serán coincidentes si comparten al menos dos puntos diferentes.
- Dos rectas se intersecan si no son paralelas y tienen un punto en común.
- Dos rectas serán coplanarias[5] si están contenidas en algún plano.
- Dos rectas son coplanarias si y solo si o bien son coincidentes o bien se intersecan o bien son paralelas.
- Dos rectas se cruzan[nota 2] si no son paralelas ni tienen puntos comunes.
Véase también[editar]
- Punto
- Segmento
- Recta numérica
- Recta tangente
- Rectas antiparalelas
- Recta de regresión
- Recta proyectiva
- Plano
- Función lineal
Notas[editar]
- ↑ También se usa rayo el cual es un posible anglicismo de ray[2] en Hispanoamérica. En algunos textos es mencionado como rayo o semirrecta[3] pero predomina el uso de semirrecta en abundante bibliografía[4] [5] [6] [7] [8] [9] que no recogen otra alternativa.
- ↑ También se dice rectas alabeadas el cual es un posible anglicismo en Hispanoamérica[3] pero predomina el uso de cruce de rectas en abundante bibliografía[13] [5] hay quien recoge la alternativa no deseada de rectas oblicuas.[14]
Referencias[editar]
- ↑ www.euclides.org: Los Elementos [1]
- ↑ Weisstein, Eric W. «Ray». En Weisstein, Eric W. MathWorld (en inglés). Wolfram Research.
- ↑ a b «Pequeña enciclopedia de matemáticas». una traducción del aleman (Pagoulatos). 1981.
- ↑ «semirrecta», Diccionario de la lengua española (22.ª edición), Real Academia Española, 2001, http://lema.rae.es/drae/srv/search?key=semirrecta.
- ↑ a b c d Real Academia de Ciencias Exactas, Física y Naturales, ed. (1999). Diccionario esencial de las ciencias. Espsa. ISBN 84-239-7921-0.
- ↑ a b Diccionario de matematicas. Akal Editores. 1979.
- ↑ Docta guia educativa. Carroggio,s.a.
- ↑ Enciclopedia didáctica de matemáticas. Oceano.
- ↑ Léxico de matemáticas. Akal Editores.
- ↑ Geometría Analítica ( 1980) Charles Lehmann; Editorial Limusa, ISBN 968-18-176-3; pg. 65
- ↑ R. Spiegel, Murray; Liu, John; Abellanas, Lorenzo (2000). «Cap 8 Fórmulas de geometría analítica plana». En McGraw-Hill Inc. Fórmulas y tablas de matemática aplicada (2 edición). Madrid: Concepción Fernández. p. 20. ISBN 84-481-2554-1.
- ↑ Wooton, William. Geometría Analítica Moderna. México 1979. P.p. 90
- ↑ «cruzar», Diccionario de la lengua española (22.ª edición), Real Academia Española, 2001, http://lema.rae.es/drae/srv/search?key=cruzar.
- ↑ Geometría(traducción). Thomson Editores Internacional.
Enlaces externos[editar]
 Portal:Matemática. Contenido relacionado con Matemática.
Portal:Matemática. Contenido relacionado con Matemática. Wikcionario tiene definiciones y otra información sobre recta.Wikcionario
Wikcionario tiene definiciones y otra información sobre recta.Wikcionario- Weisstein, Eric W. «Line». En Weisstein, Eric W. MathWorld (en inglés). Wolfram Research.
- La Recta (Español)
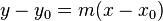
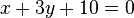
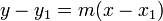
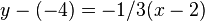
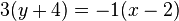
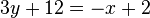
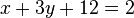

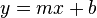
 y
y 



 :
:


 , primero se ha de calcular:
, primero se ha de calcular:
 y
y 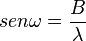 . Finalmente
. Finalmente  sin excepción.
sin excepción.

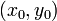 , luego tendrá que cumplirse:
, luego tendrá que cumplirse:


 , el valor de m es la pendiente de cada una de las rectas que forman parte del haz a excepción de la recta vertical por dicho punto.
, el valor de m es la pendiente de cada una de las rectas que forman parte del haz a excepción de la recta vertical por dicho punto.